coding-patterns

This is a repository of notes as I work through LEET code challenges and try to document the process to have patterns surface. It has been inspired by Parker from Interview Cake.

View on GitHub

coding-patterns to help as an aide-memoire

The idea behind this manual with accompanying code samples is to try to distill the most used algorithms and data structures that are required for coding interviews and well getting a job. But also more so that the study of algorithms and DSs should not end once one has a job, as they are really fun to play with, and they can lead to all sorts of fun places with advanced data structures and algorithms, whilst sometimes esoteric should also help you as a developer broaden your understanding and deepen your knowledge of this wonderful place called "computer land".

Online tools to practice for technical interviews

Great Courses that teach Algorithms and DS

Theprimeagen FEM Neetcode site has a course Stephen Grider course

General Programming concepts:

Be able to define, describe and demonstrate through examples the following concepts:

  1. Closure
  2. Partially applied function
  3. Currying
  4. Higher Order Functions
  5. Event loop

Will Sentance has a great course on this on the Frontend Masters platform

Javascript built-in functions and utilities to help solve coding challenges

Sorting numbers in javascript

  let numArray: number[] = [1400, 9, 80, 45];

  const sorted = numArray.sort((a, b) => a - b);

Check for presence of an array.

Because there is no native support for checking if an array exists you can use the two checks:

let isArray = []
typeof isArray === "object" && "length" in isArray // length is native in Array but not in Objects

A more robust way to check for an array is the following code:

const isArray = value => {
	return typeof value.reduce == "function" &&
	       typeof value.filter == "function" &&
               typeof value.map == "function" &&
               typeof value.length == "number";
}

Math problems and manipulating numbers

The ability to iterate through digits comes up from time to time. One effective way in python is to do the following.


    num = 12345
    lastidigit = num % 10 # 5
    firstMinusLast = int(num / 10) # 1234

This comes up in the Happy Numbers click here problem which is also solved using a slow and fast pointer, the number is slow, and the next calculation is fast. If the two meet then you have a problem (cycle), otherwise they converge on 1 which is solution.

[Product of Array except self]([https://](https://leetcode.com/problems/product-of-array-except-self/)) --- - The easy way would be to get the product of the entire array and then divide each number at the index to get value. As division is not allowed there is a less intuitive way. - It involves to passes of the array, O(n), prefix, and postfix totals are calcualated one by one as you iterate the list. - The output can be obtained by multiplying the prefix value, to the left of idx and the postfix to the right of idx. - The solution can also be done in memory O(1) as postfix and prefix can be calculated on the fly ---

prefix and postfix pattern

This is a pattern that is likely to come up often with coding interviews. The below implementation of a data structure that deals with, or utilises this pattern, where one can easily calculate prefix or postfix sums from previously calculated sub problems makes implementing solutions of this type operate in O(1) time as oppose to the brute force O(n) runtime complexity.


class PrefixSum:

  def __init__(self, nums):
    self.prefix = []
    total = 0
    for n in nums:
      total += n
      self.prefix.append(total)
  
  def rangequery(self, l, r):
    preRight = self.prefix[r]
    preLeft = self.prefix[l - 1] if l > 0 else 0
    return preRight - preLeft

Prime numbers (Primality)

The following is a reasonable way to compute prime numbers,

	primes = set()
	for a in range(2, 999):
		if all(a % p != 0 for p in primes):
			primes.add(a)

There are a number of rules for prime numbers:

  1. A prime number has only two divisors, 1 and itself
  2. Checking prime numbers before (or less than the current number) will always result in a good check to see if it divides the number. If it does then it can’t be a prime
  3. Every composite number can be factored down to a product of primes

isPrime problem

for i in range(2, floor(sqrt(n)))):
	if n % i == 0

Serializing and deserializing an Array

  PSEUDO CODE:
    - to serialise: 
        - create a result array, 
        - recursively call a dfs function, passing the next node in, and a reference to the result array to be populated inside recursive call.
        - return array as joined " ";
        Normally in the recursive call you think about the return value, and what state, in this case we only worry about the state, which is array passed in as reference.
        - base case is leaf node, if (!node) push 'x' to array and return void.
        - push the node.val and then 
        - recursively call function passing the left and right nodes in calls respectively, along with state.
    - to deserialise:
        - Use the trick of creating an iterator from the string split as array, the arr[Symbol.iterator]() will do it 
        - pass this in as the only argument to dfs function for deserialising,
        - inside the function first get the next value by calling iterator.next(),
        - if it is an 'x' char then simply return void, as its a leaf node, // base case to get out of recursion
        - otherwise create a new Node, passing parseInt(value, 10)
        - then with that node call left and right recursive calls passing result back to curr.left or curr right.
        - then return the current node, which goes back into recursive call.

    function serialize(root) {
        const res = [];
        dfs_serialize(root, res);
        return res.join(" ");
    }

    const dfs_serialize = (node, res) => {
    if (!node) {
        res.push("x");
        return;
    }
    res.push(node.val)
    dfs_serialize(node.left, res)  
    dfs_serialize(node.right, res)
    }

    function deserialize(s) {
        return dfs_deserialize(s.split(" ")[Symbol.iterator]())
    }

    const dfs_deserialize = (nodes) => {
        const {value} = nodes.next();
        if (value === "x") return;
        const newNode = new Node(parseInt(value, 10))
        newNode.left = dfs_deserialize(nodes)
        newNode.right = dfs_deserialize(nodes)
        return newNode;
    };

General Patterns to start solving a problem

Calculating complexity

Describe Big O (three points): * growth is with respect to the input * Constants are dropped * Worst case is expected in interview settings

Specific patterns to solving a problem

Python tips and tricks commonly used

generate an empty multidimensional array using a list comprehension of size n --- ```python freq = [[] for n in range(len(n) + 1)] ``` ---
update an item in a dict, and add a first entry if it is not present --- ```python dict[n] = 1 + dict.get(n, 0) ``` ---

Be aware of immutable updates to a string variable in a for loop. Rather use a List which is mutable and later pass back a string.

image

  # get rid of slice calls in recursion. bake in an extra argument called i
  def _non_adjacent_sum(nums, 0):
      # change base case to deal with index increasing
      if i >= len(nums):
         return 0
      # deal with recursion on index and not slicing array each time
      include = nums[0] + _non_adjacent_sum(nums, i + 2) # avoid the adjacent value
      exclude ....

The complexity of this approach would be O(n) time and O(n) space. Both linear time.

Usually to calcualte the complexity you first drwa out the state-space decision tree and then you can see how many decisions you have to make, this will be your coefficient. and then the height of the tree would be your factor.

To take an example to demonstrate this as well as the alternative approach of Bottom UP or Tabulation the below Climbing Stairs problem has been used. The Bottom up approach can result also in O(n) runtime but using two vars to keep track of previous sub-problems that were calculated you can reduce the space complexity to O(1), constant time.

Image

The below is the DFS recursive with memoisation solution Time: O(n) Space: O(n)

def _climbStairs(n, memo):
    
    if n in memo:
        return memo[n]
    
    if n < 0:
        return 0
    
    if n == 0:
        return 1
    
    memo[n] = _climbStairs(n - 1, memo) + _climbStairs(n - 2, memo)
    return memo[n]
    
class Solution:
    def climbStairs(self, n: int) -> int:
        return _climbStairs(n, {})

The below is the bottom-up Time: O(n) Space: O(1)

class Solution:
    def climbStairs(self, n: int) -> int:
        one = 1
        two = 1
        for i in range(n - 1):
            one, two = one + two, one
        return one

TODO ADD MIN COST CLIMBING STAIRS STEPS

Describe pseudo steps to solve min cost problem? + This is solved using a bottom up, DP solution + It result in O(n) time and O(1) space + Start at third to last item in list, and iterate backwards until -1 + keep adding the min amount and step once or step twice + finally return the minimum of first or second value #### Python code ```python class Solution: def minCostClimbingStairs(self, cost: List[int]) -> int: cost.append(0) for i in range(len(cost) - 3, -1, -1): cost[i] += min(cost[i + 1], cost[i + 2]) return min(cost[i], cost[i + 1]) ```

Algorithms to know

Max value logic implementation

In javascript it is similar but different syntax

  Math.max(left, right)
  Math.min(left, right)
  // and use the defualt Inifinity or -Inifinity
  Inifinity || -Inifinity

Two pointers

            const uncompress = (s) => {
            
            let left = 0;
            let right = 0;
            const output = [];
            
            const isNumber = new RegExp(/\d/)
            
            for (let i = 0; i < s.length; i++) {
                if (isNumber.test(s[i])) {
                    right += 1;
                    continue;
                }
                const times = s.slice(left, right);
                output.push(s[i].repeat(times));
                left = right + 1;
                right = left;
            }
            
            
            
            return output.join('')
            };


            uncompress("2c3a1t");

Two pointers come in a number of forms: - same direction (used for Remove duplicates), or fast, slow pointers. - opposite direction (used for Two sum sorted) - sliding window (used for Longest substring without repeating characters) - Prefix sum

The key to using two pointers pattern in a two sum type problem is knowing the porerties of the sorted array. It is such that by setting the L and R bounds on the boundaries, you can work on the fact that if the sum of these two values is greater than the target, then no matter what L values you add will the sum get smaller, only bigger. SO you need to decrement the R value, and look in the smaller side of the array. Ditto if the sum is smaller, no R value to the left will make it bigger, and so you need to move the L value to the right (i.e. look for a bigger value). This property and the fact that there is always one solution means you can solve this in O(n) time. The condition where L oversteps the R bound will never be reached and you only then need one return statement in the while loop once the sum == the target, then return the L and R indexes.

Sliding window pattern with example

####Longest Repeating Character Replacement


    def characterReplacement(self, s: str, k: int) -> int:
        
        # Hashmap to record number of occurances of a char
        count = {}
        # 1/ Set the left pointer of sliding window
        l = 0
        # highest count of non-repeating chars so far replaced
        res = 0
        
        # 2/ right pointer moves through string starting at 0
        for r in range(len(s)):
            # Hashmap hack to set initial value to 0 if does not yet exist, otherwise increase count of char
            count[s[r]] = 1 + count.get(s[r], 0)
            
            # 3/ Condition to decrease sliding window from the left
            # if the width of windw minus the highest occuring char count is greater than allowed chars to replace then decrease the count of left char, and move left pointer inwards, decrease size of window so the count is still valid
            if (r - l + 1) - max(count.values()) > k:
                count[s[l]] -= 1
                l += 1
            # Check if we have a higher count
            res = max(res, r - l + 1)
        return res

Two pointers often allows us to move from the brute force solution of nested for…loops O(n^2) to a more efficient linear time complexity of O(n) passing only once through iterable data structure.

###Find all anagrams

see Find all anagrams file

### Two Sum II Sorted array

### Three Sum problem

The python solution is below with pseudo code:

Best time to buy / sell stock

    def maxProfit(self, prices: List[int]) -> int:
        # two ptr, sliding window for time based problems which can only go in one direction
        # initiliase two ptrs, one l for buy, and one right for sell after the l ptr
        l, r = 0, 1
        maxProfit = 0
        # iterate over prices array once so O(n) is time complexity
        while r < len(prices):
            # if its a profitable trade
            if prices[l] < prices[r]:
                #calculate profit
                profit = prices[r] - prices[l]
                # is it current max
                maxProfit = max(maxProfit, profit)
            # only slide l ptr if there is a lower buy price in the future, move it then to lowest price
            else:
                l = r
            r += 1
        return maxProfit

<p style="color:lightgreen">Kadanes Algorithm<p>

This is an algorithm that mirrors or has overlap with the sliding window pattern and some form of dynamic problem in that it considers the previous sub problems results.

The brute force solution often intuitively formed is to create a O(n^2) solution, or nested for loops to work out the solution. But this can be improved to a O(n) solution using Kadanes Algorithm.

The solution is deceptively simple, although to work it out is not as simple.

If we take the following problem example:

  Calculate the maximum sum of the largest sub array given an array of n numbers, which could be postive or negative, [1,-2,-3,5,7,-12,4,5]

The algorithmic thinking steps

  1. Start by defining a variable to hold the maximum sum so far, because we cannot have an empty sub-array we can default the maximum sum so far to the first value in the array so nums[0]
  2. Declare a variable to hold the currSum value, default it to 0
  3. Iterate over the array and keep growing the window.
  4. Inside the iteration step check if currSum is the maximum with 0, i.e. its greater than 0. We can never have a negative currSum which will make the next addition of the array value bigger. If currSum is negative we reset the currSum with the current array[n] value
  5. we check if maxSum is overtaken by the new currSum value
  6. upon exiting the for..loop we return the maximum sum found.

See Kadanes algorithm file

<p style="color: lightgreen"> Linked Lists </p>

Know the default implementation to recurse a linked list. It can be done iterative, or recursively. While the recursive solution is more elegant it does consume O(n) space as each call is placed on the call stack.

# iterative core pattern for traversal

def traverse(head):
   
   current = head
   while current is not None:
      # do something with node
      current = current.next

Also know the dummy node, or recursive index tracking logic for adding nodes

class Node:
  def __init__(self, val):
    self.val = val
    self.next = None
# Iterative solution with dummy head logic
# def create_linked_list(values):
  
#   dummy = Node(None)
#   tail = dummy
#   for val in values:
#     tail.next = Node(val)
#     tail = tail.next
#   return dummy.next
  
# recursive solution avoids dummy head logic, but make sure 
# to include index tracking logic to avoid O(n2) from slicing a values array
def create_linked_list(values, i = 0):
  if i == len(values):
    return None
  head = Node(values[i])
  head.next = create_linked_list(values, i + 1)
  return head

Sum list problem

Remove Nth Node from end of list

<p style="color: lightgreen">Find middle node of linked list</p>

This solution uses a fast and slow pointer, the fast pointer moves twice as fast, which intuitively means the slow pointer will be half way to the end, then return the slow pointer’s val when fast pointer hits end of linked list.

               class Node {
                   constructor(val, next = null) {
                       this.val = val;
                       this.next = next;
                   }
               }

               function middleOfLinkedList(head) {
                   let slow = fast = head;
                   while (fast && fast.next) {
                       fast = fast.next.next;
                       slow = slow.next;
                   }
                   return slow.val;
               }

Remove linked list elements ♻️ ✔️ 🔗

Add two numbers

Reverse a linked list

- THE TRICK TO KICK THIS OFF, THINK OF REVERESING THE ARROWS, START WITH FIRST node arrow pointing to the left to a created dummy ndoe, prev
- This can be done iteratively or recursively. The iterative approach is more space efficient.
- Start with a prev node set to null or None
- setup up classic iteration. Foundational code for traversing LL
- inside while loop store current.next node in a temp var
- assign the current.next to prev node
- move prev node to current node
- advance current node to next (temp var ) node

Here is python code:

   def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        
        prev = None
        current = head
        while current is not None:
            next = current.next
            current.next = prev
            prev = current
            current = next
            
        return prev

Remove a node from linked list

The below is the normal deletion given a head node to traverse. The leet code problem only gives you the actual node to delete. Trick question really, but solved in two lines of code.

# class Node:
#   def __init__(self, val):
#     self.val = val
#     self.next = None

def remove_node(head, target_val):
  # The below is the edge case for when the first node is the target
  if head.val == target_val:
    return head.next
  current = head
  # Gotcha 1: Make sure its None and not an Empty Node Node(None)
  prevNode = None
  while current is not None:
    if current.val == target_val:
      # Gotcha 2: Must be assigning prevNode.next to current.next, and not prevNode = current.next
      prevNode.next = current.next
      break  
    prevNode = current
    current = current.next
  return head

Union find data structure

These are also known as Disjoint sets. This data structure can be used to detect a cycle in a graph. The reason they are also called union find is because of the two methods the DS commonly implements namely, union and find.

The idea is to think about it as a set like a tree datastructure, if an element shares the root node it can be considiered part of the set, if it does not then it is disjoint.

To determine if there is a cycle, if you connect edges, and they are already connected in your union find DS, then you have a cycle.

see union_find.py file to see implementation.

The time complexity without further optimisations is going to be O(n) time. But the optimisation made in the Union-find DS usually includes the two following code optimisations:

  1. path compression, this is added in the find method of the class.
  2. find by rank

** Implementing ** just one of these would lead to a time complexity of O(log n), but implementing both optimisations would get to O(1). The mathematical reason or proof comes from inverse ackerman. O(α(n))

Floyds cycle finding algorithm

This algo uses the two pointer pattern on a linked list to detect if there is a cycle. A slow pointer and a fast pointer The base case is if fast pointer reaches end of linked list, ie hits a None, then it is not a cyclic LL

##### Fast and Slow pointers (expanded) The fast and slow pointer pattern can be expanded to understandnig the algorithm to solve the problem where you are asked to find the head of a cycle in a linked list. The algorithm is simple but not intuitive. It can be solved with a math proof though.

The general idea is that you use a fast and slow pointer in the usual way to detect a cycle. Once the cycle is detected then you break from this loop and do a final check of the terminating condition, i.e. if your fast pointer reached the end of the list, as there was no cycle detected. Once it is sure there is a cycle, then you introduce a second slow pointer a tthe head. The original slow pointer is still pointing to its original location which is the point at which the fast and slow pointers met. So the fast pointer had done a full cycle of the cycle and then intersected the slow pointer. Setting up a second while loop, with a terminating conditon being when the slow one and slow two pointers meet that is the point or the head of the cycle.

This can be understood in a math proof below:

    2 * (p + c - x) = p + c + c - x
    slow pointer       fast pointer
    using algebra, the above forumula is simplified down to 
    p = x

    p = distance before cycle detected
    c = distance of cycle
    c - x = distance between head of cycle and where intersection happened.

A problem where this is used to solve is called Happy Number

Pattern for connecting nodes in a linked list recursively


def connect(node: Node):
	if node is None:
		return None
	newNode = Node(node.val + some logic)
	newNode.next = connect(node.next)
	return newNode

<p style="color: lightgreen">Sorting Algorithms</p>

Bubble Sort

Whiteboard a bubble sort alogorithm and code it in your favourite language? 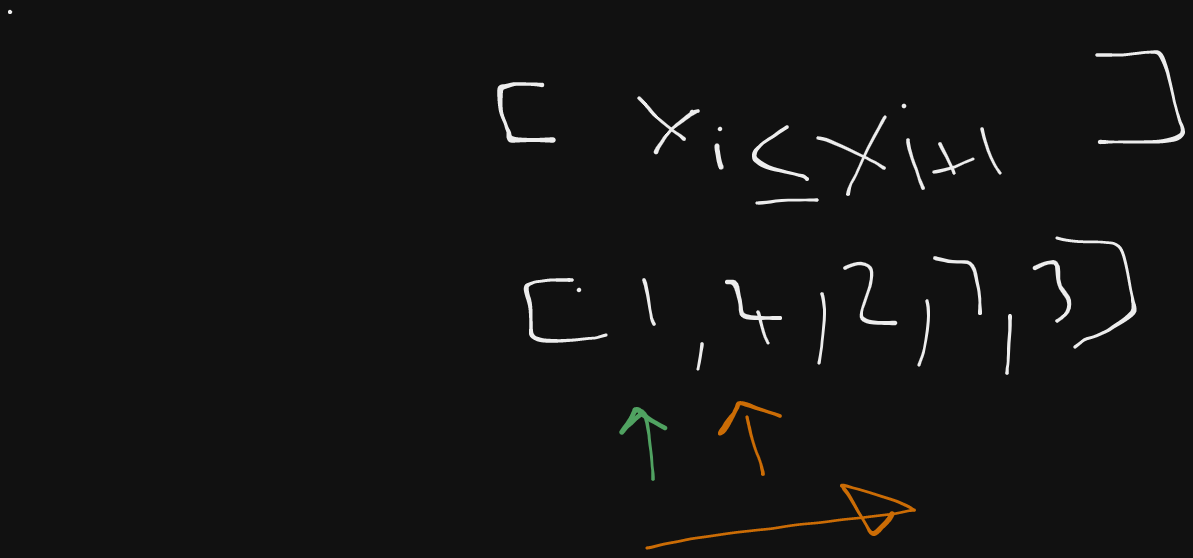![Picture of the bubble sort algorithm](/coding-patterns/bubble_sort.png) - Running time is O(n^2) because of property of summing a range of numbers formula - N + 1 * N / 2 = N2 + N = N2 - Iterate through the list, and compare the the next two adjacent elements - Stop when only one element left to sort, one lement in array always sorted ```python for (let i = 0; i < arr.length; i++) { for (let j = 0; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1]) { const tmp = arr[j] arr[j] = arr[j + 1] arr[j + 1] = tmp } } } ```

Insertion sort

            function sortList(unsortedList) {
                
            // insertion sort algorithm
                for (let i = 1; i < unsortedList.length; i++) {
                let current = unsortedList[i];
                let j;
                for (j = i - 1; j >= 0 && unsortedList[j] > current; j--) {
                    unsortedList[j + 1] = unsortedList[j];
                }
                unsortedList[j +1] = current;  
                }
                
                return unsortedList;
                
            }

#### <p style="color: lightblue">Merge sort</p>


            const unsortedArr = [31, 27, 28, 42, 13, 8, 11, 30, 17, 41, 15, 43, 1, 36, 9, 16, 20, 35, 48, 37, 7, 26, 34, 21, 22, 6, 29, 32, 49, 10, 12, 19, 24, 38, 5, 14, 44, 40, 3, 50, 46, 25, 18, 33, 47, 4, 45, 39, 23, 2];

            function merge<T>(s: T[] ) {
            // base case for recursive function. i.e. if it is one item in array, array is sorted.
            if (s.length <= 1) {
                return s;
            }
            // divide and conquer, split array in half
            const mid = Math.floor(s.length /2);
            const left = s.slice(0, mid);
            const right = s.slice(mid);
            // recursive case, keep calling merge function until sub-arrays are split over and over
            const left_sorted: any = merge(left);
            const right_sorted: any = merge(right);
            // perform the sorting step using the utility function which merges two sorted arrays. This returns many of the sub arrays sorted
            return _mergeSortedArrays(left_sorted, right_sorted);

            }

            function _mergeSortedArrays<T>(a: T[], b: T[]) {
                
                const sorted = [];
                // keep finding the smallest element between the two sorted arrays. The shift operation removes the first element, thus making array
                // smaller and adhering to while loop condition
                while (a.length && b.length) {
                sorted.push(a[0] <= b[0] ? a.shift() : b.shift() );
                };

                // this is a short-cut, using ES2106 syntax, it spreads the sorted array, and concatenates the remaining two arrays. Because
                // the condition above in the while loops guarantees only one array could still cnotain values, we can safely spread both arrays
                // which will either append all remaining from one of the arrays and append an empty array which has no effect.
                return [...sorted, ...a, ...b];
            };

            console.log(merge(unsortedArr))


    function findMinRotated(arr) {
    let left = 0;
    let right = arr.length - 1;
    let boundary_index = -1;
    while (left <= right) {
        let mid = left + Math.trunc((right - left) / 2);
        // if <= last element, then belongs to lower half
        if (arr[mid] <= arr[arr.length - 1]) {
            boundary_index = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return boundary_index;
}

Peak of mountain array

Topological order

Data Structures

Queue

Stack

Trees

### What is a tree data structure It is a data structure with the following properties: + nodes connected by edges, the edges are always N - 1, so if 7 nodes, 6 edges. + node can have any data type as values + nodes can be connected to 0 or more child nodes (depending on type of tree) + each child node must be connected to exactly one parent + this constrains trees to be acyclic 
  // TEMPLATE FOR DFS on TREE
    function dfs(node, state) {
        if node is null
          ...
          return
        left = dfs(node.left, state)  
        right = dfs(node.right, state)  
        ...
        return ...
    }

Balanced binary tree

Binary tree

Comparing python code to javascript code for max root to leaf problem
def max_path_sum(root):
  
  if root is None:
    return float("-inf")
  
  if root.left is None and root.right is None:
    return root.val
  
  maxLeft = max_path_sum(root.left)
  maxRight = max_path_sum(root.right)
  
  return root.val + max(maxRight, maxLeft)

function maxPath(root)
... TODO

Tree path finder problem

def path_finder(root,target):
  result = _path_finder(root,target)
  if result is None:
    return None
  else:
   # neat python reverse list syntax
   return result[::-1]
#using the convention of underscore to say this is internal function, not to interfere in coding challenge function calling correct signature above
def _path_finder(root, target):
  
  if root is None:
    return None
    
  if root.val == target:
    return [ root.val ]
  
  left = _path_finder(root.left, target)
  if left is not None:
    left.append(root.val)
    return left
  
  right = _path_finder(root.right, target)
  if right is not None:
    right.append(root.val)
    return right
  
  return None

Tree levels problem

DFS Return all node values

* __iterative__
    - Either iteratively, use a stack to push the root node
    - Then while stack.length then push value onto values array
    - recursively call dfs for left and right nodes if they exist
    - finally return values array.
* __recursive__ 
    - think about your return values. in this case its an array
    - base case is empty node, return empty array.
    - return the value, then spread out the collection of dfs calls on left and then right.

    const depthFirstValues = (root) => {
      return dfcount(root)
    };

    const dfcount = (node) => {
      if (!node) return [];
      return [node.val, ...dfcount(node.left), ...dfcount(node.right)]
    }

Breadth First Search and iteration on Binary trees

Lefty nodes problem

Sum of left Leaves ♻️ ✔️

Binary Tree Inorder traversal

Lowest common ancestor

** See the python file at (./lowest_common_ancestor.py) for a solution

Another elegant solution to the problem is below

    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        curr = root
        while curr:
            if p.val < curr.val and q.val < curr.val:
                # go down the left sub tree
                curr = curr.left
            elif p.val > curr.val and q.val > curr.val:
                #go down right subtree
                curr = curr.right
            else:
                #we are at the branch, of LCA
                return curr

Binary Search trees

Valid Binary Search Tree

    Pseudo Code
    1. think about return values, i.e. all same type of boolean being bubble up through tree. true && false
    2. Think about state that needs to be mainteind through each recursive call, the min and max value range for a node to be BST true
    3. Try not to nest your resucrsive function in main function to avoid namespace collisions and call stack errors.

        function dfs(node, min, max) {
            
                if (!node) return true;

                if (!(min <= node.val && node.val <= max)) return false;
                return dfs(node.left, min, node.val) && dfs(node.right, node.val, max);
            }

        function validBst(root) {
            return dfs(root, -Infinity, Infinity) 
        }

<p style="color: lightgreen">Invert BST</p>

    function invertBinaryTree(node) {
        if (!node) return;
        return new Node(node.val, invertBinaryTree(node.right), invertBinaryTree(node.left));
    }

<p style="color: lightgreen">kth smallest number</p>

        function kthSmallest(bst, k) {
        let count = 0;

        const dfs = (node, k) => {
            if (!node) return null;
            let left = dfs(node.left, k);
            if (left) return left;
            count++;
            if (count === k) return node.val;
            return dfs(node.right, k);  
        }
        return dfs(bst, k);  
        }

Breadth first search, return level order elements in a multidimensional array

        function levelOrderTraversal(root) {
            
            const queue = [root];
            const result = [];
            while (queue.length) {
                const level = [];
                const n = queue.length
                for (let i = 0; i < n; i++) {
                const node = queue.shift();
                level.push(node.val);
                for(let child of [node.left, node.right]) {
                    if (child) queue.push(child);
                }
                }
            result.push(level);  
            }
            return result;
        }

Zizag level order traversal(https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/)

This is the same as above with some slight changes (adding a boolean flag)

Heap

A heap data structure is a type of binary tree, which is mostly complete. Being mostly complete (i.e. leaf nodes are on the far left) allows for O(log n) lookup, and O(log n) insert and delete. A min and max heap, means the heap is mostly sorted, all levels are sorted, but not necessarily the values oneach level. This allows one to quickly start at the top (min heap will be smallest to largest going down) and find the node you are looking for, the real power over a normal a sorted array is that the insert and delete

A common abstract data type (ADT) called a priority queue is used under the hood for implementing the actual heap datastructure. In python one can import the PriorityQueue class from Queue or import the functions heapify, heappop, heappush from heapq package to create a heap. start with heap = [].

The below problem of MergeKSortedLists is solved using the builtin heap in python.

from heapq import heappop, heappush
from typing import List

def merge_k_sorted_lists(lists: List[List[int]]) -> List[int]:
    res = []
    heap = []
    for curr_list in lists:
        heappush(heap, (curr_list[0], curr_list, 0))
    while heap:
        val, curr_list, index = heappop(heap)
        res.append(val)
        index += 1
        if index < len(curr_list):
            heappush(heap, (curr_list[index], curr_list, index))
        
    return res

Min cost to connect all points

This is solved in a maximally efficient way using Prims algorithm

It is expected to understand the properties of a minimum spanning tree:

It is an acyclic undirected graph. The number of edges will always be n - 1, where n is the number of nodes or vertices.

One needs to build an adjacency list, so knowing this is important, additionally the structure of Prims algorithm: The time complexity is O(n2.logn)

Practically the following is necessary:

Graphs

  • A depth first search of a graph uses a stack data structure behind the scenes
  • A breadth first search of a graph uses a queue data structure behind the scenes
  // Usually take in an adjacency list as input.
  {
      a: [b,c],
      b: [d],
      c: [b, e],
      e: []
  }
// but it can also take and edge list, which needs to be converted to an adjacency list first
// A list where the index represents the node and the value at that index is a list of the node's neighbors:
  const graph = [[0, 1], [1, 2], [1, 3], [2, 3]];

Think from the point of a node

edge list to adjacency list

The terminology differs slightly with trees. When talking about graphs we say vist each neighbor, as technically they are not children like in trees which have a acyclic top down structure.

Graph traversals

Depth first traversal

- directed graph, follow the vertices all the way to a node with no neighbors
- Uses a stack under the hood (FILO)

Breadth first traversal

- Uses a queue under the hood (FIFO)
-

Path finding

Cyle detection algorithm

Generic cycle detection algo

   const shortestPath = (edges, nodeA, nodeB) => {
     const graph = buildGraph(edges)
     // 1. ADD VISITED SET INITIALISED WITH FIRST NODE IN BRACKETS
     const visited = new Set([nodeA])
     // 2. PASS IT ALONG IN ALL BFT CALLS
     bft(graph, nodeA, visited)
   };

   const bft = (graph, node, visited) => {

     const queue = [node];
     while(queue.length) {
       const node = queue.shift();
       for(let neighbor of graph[node]) {
         // 3. DO THE CHECK ONLY AT THE TIME YOU WOULD ADD IT TO THE QUEUE
         if (!visited.has(neighbor)) {
           queue.push(neighbor)
           // 4. ADD IT TO THE VISITED SET AS WELL AFTER ADDING TO QUEUE
           visited.add(neighbor)
         }
       }
     }
   }


   const buildGraph = (edges) => {
     const graph = {};

     for(let pair of edges) {
       const [a,b] = pair;
       if (!graph[a]) graph[a] = [];
       if (!graph[b]) graph[b] = [];
       graph[a].push(b)
       graph[b].push(a)
     }
     return graph;
   }

   const edges = [
     ['w', 'x'],
     ['x', 'y'],
     ['z', 'y'],
     ['z', 'v'],
     ['w', 'v']
   ];

   shortestPath(edges, 'w', 'z'); // -> 2

<p style="color: lightgreen">Depth first traversal</p>

<p style="color: lightgreen">Breadth first traversal</p>

      
      const graph = {
        0: [1, 2],
        1: [0, 2, 3],
        2: [0, 1],
        3: [1]
      }
 
     function shortestPath(graph, r, c) {
        
            const queue = [[r, 0]];
            const visited = new Set([r]);
            while (queue.length) {
              const [node, distance] = queue.shift();
              if (node === c) return distance;
              for(let neighbor of graph[node]) {
                  if (!visited.has(neighbor)) {
                    visited.add(neighbor)
                    queue.push([neighbor, distance + 1]);  
                  }
               }
            }
      }
    
    shortestPath(graph, 0,3))

<p style="color: lightgreen">Dijkstras (shortest path)</p>



## <p style="color: lightgreen">Island hopping logic</p>
  - You will need a graph in the form of an object where the keys are nodes and the values are adjacency lists.
  - You get access to the adjacency lists and are inclusive of all islands by using the <code>for ... in call</code> on the graph.
## <p style="color: lightgreen">Grid Graph problems</p>
Sometimes you will be presented with a grid graph, such as 

[
    [W,W,L,W],
    [L,W,L,W],
    [W,W,L,W],
    [L,L,L,W],
    [L,W,L,W],
    
] ```

This pattern appears for problems such as flood fill or connected islands problem.

A good way to visualise this is to think about the delta_row and delta_col as something akin to the following: | | r - 1 | | |——–|——–|——–| | r + 0 | r | c + 1 | | c - 1 | c | r + 0 | | | r + 1 c + 0 | |

The idea is then that you go in a clockwise direction and place these in a delta array,

	delta_row = [-1, 0, 1, 0]
	delta_col = [0, 1, 0, -1]

DEBUGGING RECURSIVE CASES A common gotcha with recursive cases where you have defined your base case correctly but still get stack overflow errors, is where you are off by one in your counting logice or in or out of bounds checks, very, very carefully reason about these and usually this will solve the issue.

        /* 
        #1 Iterative code as part of main algorithm
        #2 Cycle detection logic
        #3 Recursive logic to visit all neighbours
        
        */
        const islandCount = (grid) => {
        let count = 0;
        //#2 declare an empty set to store string representation of r + c locations
        const visited = new Set();
        
        //#1 iterate with nested for loops
        for(let r = 0; r < grid.length; r++) {
            for(let c = 0; c < grid[0].length; c++) {
            //#3 call it first time to kick things off
            // returns true or false, if true it means we have an island
            if (explore(grid, r, c, visited)) count += 1;
            }
        }
        return count;
        };


        const explore = (grid, r, c, visited) => {
        //#1 check if we are going outside of the grid graph at any point
        const rowInBounds = 0 <= r && r < grid.length;
        const colInbounds = 0 <= c && c < grid[0].length;
        if (!rowInBounds || !colInbounds) return false;
        
        //#3 first base case, if we have got to a dead end
        if (grid[r][c] === 'W') return false;
        
        const pos = `${r},${c}`
        if (visited.has(pos)) return false;
        visited.add(pos);
        
        //#3 recursively call the function on all the neighbors going up down, left and right
        explore(grid, r + 1, c, visited)
        explore(grid, r - 1, c, visited)
        explore(grid, r, c + 1, visited)
        explore(grid, r, c - 1, visited)
        
        //#1 if the call gets to this point then we can return true as we have succesfully traversed 
        // a L land island.
        return true;
        }


        const grid = [
        ['W', 'L', 'W', 'W', 'W'],
        ['W', 'L', 'W', 'W', 'W'],
        ['W', 'W', 'W', 'L', 'W'],
        ['W', 'W', 'L', 'L', 'W'],
        ['L', 'W', 'W', 'L', 'L'],
        ['L', 'L', 'W', 'W', 'W'],
        ];

        islandCount(grid); // -> 3

<p style="color: lightgreen">Bipartite graphs and graph coloring</p>

<p style="color: hotpink">Hash maps</p>

Contains Duplicate

Given an integer array nums, return true if any value appears at least twice in the array, and return false if every element is distinct. - In order to know if every value is unique you need to iterate at least once - You can check if you have seen the digit before by storing each element in a **hash map** - Then you will possibly exit early, but worst case is O(n) - See Leet code submission for answer.

Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise - uses a **hashmap**, use the Counter class to construct a dict, or for...in over first string - for...in over second string and decrement count if char found, if its 0 use del keyword to remove element. - return check of len(dict) == 0, i.e. all chars used and both input strings *( edge case )* the same

Two Sums Problem

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target. - The brute force approach suggests two for loops giving 0(n2) - the introduction of a hash or map allows one to capture the value as the key in the kv store which later can be checked if the complement (i.e. the difference) between target value and the value being iterated. - create an empty dictionary, enumerate over nums, get difference, check if its in the dict - if its in the dict return its value (is index of complement), and the current index (i) - each iteration then also add the current value as key, and current index as value in KV pair. - NOTE THE ABOVE STEP, Its a tricky gotcha, make sure to add the current value, NOT the complement.

Group Anagrams

Given an array of strings strs, group the anagrams together. You can return the answer in any order. - identify the datastructure required, which is a hashmap mapping charCount -> list of Anagrams - Deal with the edge case of index out of bounds by using a defaultdict(list) instead of the usual {} dict. - To keep a unique key of each word, create a array initialised to 0s for each character in the alphabet - then inside the for loop for each word, check each character and increase the count of each character in the 0...25 list, giving you a unique signature for each word. - This key will match every other word or anagram uniquely. NOTE store it as a tuple so as to be able to reference it as a key. - finally after looping through the list of words return the resulting dict's values() as answer - This can be solved in O(m * n) ```python def groupAnagrams(self, strs: List[str]) -> List[List[str]]: # use to store lists of words res = defaultdict(list) # check each word for s in strs: # for every word, create a 0...25 array initialized to 0s count = [0] * 26 # check each char in the word, and update the 0...25 list increasing occurence of char for c in s: count[ord(c) - ord("a")] += 1 # count is now a unique signature to identify anagrams, typecast it to tuple so it can be used as a hashing key # append the anagram words at each unique signature, giving your dict of lists res[tuple(count)].append(s) # return the lists stored in values, giving a list of lists return res.values() ```

Top K Frequent Elements

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order. - This can be solved using a max Heap, but less intuitively also using a modified bucket sort - The idea is to use the index of the bucket sort array as the count and the values as an array which holds the nums that appear n number of times as per the correct index value - You will need a hashmap, array of arrays, and a result array. - You need to know how to **generate an empty multidimensional array using a list comprehension of size n** - You need to know how to **iterate over list backwards** - YOu need to know how to **update an item in a dict, and add a first entry if it is not present** ```python count = {} freq = [[] for n in range(len(nums) + 1)] for n in nums: count[n] = 1 + count.get(n, 0) for n,c in count.items(): freq[c].append(n) res = [] for i in range(len(freq) - 1, 0, -1): for n in freq[i]: res.append(n) if len(res) == k: return res ```
[Longest Consecutive Sequence](https://leetcode.com/problems/longest-consecutive-sequence/) - Convert list to a set - Iterate through list, does it have a left neighbour (i.e. one less then num) - if yes, while the length = 0, one less than num + length, increment length by 1 - check max(current longest, and stored longest) - return longest --- answer ---

<p style="color: hotpink">Dynamic Programming patterns</p>

Recursion (top-down, with memoization)

Two things to decide on when thinking through recursion

  1. The return value (passing value up from child to parent)
  2. Identifying the state (passing value down from parent to child)

In essence when solving a problem with recursion either use the return value (partition and merge) or store a global variable that is updated based on each recursive call.

brute force

Duplicate value avoidance pattern

0 1 1 2 3 5 8 problem 🗃️ Dynamic Programming using recursion with memoization, or bottom up.

Dynamic programming - Dynamic number of subproblems

Sum Possible problem

Summing Squares

Image

(./summing_squares.py) for solution

###Minimum perfect squares

    var numSquares = function(n, memo = {}) {
        
        if (n in memo) return memo[n];
        
        if ( n === 0 ) return 0;
        
        let min = Infinity;
        for (let i = 1; i <= Math.sqrt(n); i++) {
            const square = i * i;
            const squares = 1 + numSquares(n - square, memo);
            min = Math.min(min, squares);
        }
        
        return memo[n] = min;
};

Knapsack weight only

Longest increasing subsequence

         function longestSubLen(nums) {
             // kick the recursive calls off, 
             // pass in the array, the ith index starting at begining of array,
             // the length of the array, as this is used to decide the base case, reaching end of array.
             // and start with -Infinity so that at least first element is included in count
             return calculate(nums, 0, nums.length, -Infinity)
         }
          
         const calculate = (arr, i, n, prev) => {
           // base case return 0 once end of array reached
           if (i === n) return 0;

           // either exclude current value, and recursively call
           let exclude = calculate(arr, i + 1, n, prev)
           
           // or include it only if the value is actually greater than previous value
           let include = 0;
           if (arr[i] > prev) {
             include = 1 + calculate(arr, i + 1, n, arr[i])
           }
           // finally return the current max value.
           return Math.max(exclude, include)
         }

longest Subsequence palindrome

Image

Python solution is (./longest_subsequence_palindrome.py)

Triangle [dp, recursion, memoization]

      /**
       * @param {number[][]} triangle
       * @return {number}
       */
      var minimumTotal = function(triangle) {
          
          // the recursive function inside main function to close over the triangle 2D array.
          
          const dfs = (i,level, memo = {}) => {
              
              // memoization requires both the ith position in sub array and level. 
              const pos = `${i},${level}`;
              // base case once recursion reaches bottom level of triangle, or last subarray entry
              if (level === triangle.length) {
                  return 0
              }
              
              if (pos in memo) return memo[pos]
              
              
              const next_level = level + 1;
              // magic happens here, return the minimum of the ith and ith +1 index, plus last known value.
              return memo[pos] = Math.min(dfs(i, next_level, memo),
              dfs(i + 1, next_level, memo)) + triangle[level][i]
              
          }
          // kick off recursion starting at top of triangle
          return dfs(0,0);
      };

      minimumTotal(
      [[2],[3,4],[6,5,7],[4,1,8,3]]) // 11

<p style="color:lightgreen">Combinatorial search on trees</p>

Think about the problem as using a binary tree as a framework to generate all possible subsets. Whilst you don’t code the Binary tree nodes, you can use the same recursive DFS techniques to visit all the possible combinations.

Working out the big O complexity for maximum recursion (all possible combinations)

def subsets(elements):
  
  if len(elements) == 0:
    return [[]]
  
  first = elements[0]
  subs_without_first = subsets(elements[1:])
  subs_with_first = []
  for sub in subs_without_first:
    subs_with_first.append([first, *sub])
  
  return subs_without_first + subs_with_first
  
  
subsets(['a', 'b', 'c']) # ->
# [
#   [],
#   [ 'c' ],
#   [ 'b' ],
#   [ 'b', 'c' ],
#   [ 'a' ],
#   [ 'a', 'c' ],
#   [ 'a', 'b' ],
#   [ 'a', 'b', 'c' ]
# ]
Backtracking template pseudocode
    function dfs(node, state) {
        if __state__ is a solution {
            report(state) // add state to final result list
            return
        }

        for (child of children) {
            if child is a part of a potential solution
            state.add(child) // make move
            dfs(child, state)
            state.remove(child) // backtrack
        }
    }
Javascript code to demonstrate above backtracking
    function dfs(root, path, res) {
        if (root.children.every(c => !c)) {
        res.push(path.join("->"))
        return;
        }
        
        for (let child of root.children) {
        if (child) {
            path.push(child.val);
            dfs(child, path, res);
            path.pop();
        }
        }
    }

Backtracking can also be applied to aggregation type problems. The below pseudo code template can be applied to these types of problems:


function dfs(start_index, [...additional states]):
	if is_leaf(start_index):
		return 1
	ans = initial_value
	for edge in get_edges(start_index, [...additional states]):
		if additional states:
			update([...additional states])
		ans = aggregate(ans, dfs(start_index + len(edge), [...additional states])
		if additional states:
			revert([...additional states])
	return ans

Solving the permutation problem with pseudocode

  1. Identify the states, so you need to know the full path, and when it has been reached to record this, pass it along, and second state is to know which letters have been used.
  2. DRAW THE TREE (State-space-tree).
  3. Apply DFS and backtrack template.
    • base case is when path.length == letters.length
    • then append the path to res (found one path), and return
    • then for over the letters and check if used, continue, otherwise path.push the letter, mark it as used and recursively call the dfs function.
    • then backtrack, pop letter from path and mark letter[i] as false
    • finally call the function first time, passing [] for path, Array(letters.length).fill(false) and return res
    function permutations(letters) {
        const res = [];
        dfs([], Array(letters.length).fill(false), res)
        return res;
        
        function dfs(path, used, res){
            if (path.length === letters.length) {
            res.push(path.join(""));
            return;
        }  
        for(let i = 0; i < letters.length; i++) {
          if (used[i]) continue;
          path.push(letters[i]);
          used[i] = true;
          dfs(path, used, res);
          path.pop();
          used[i] = false;
        }
        return res;
    }
  }

### Letter Combinations problem

Count paths problem

Coin Change

This is part of the sequence type DP problems. The below solution uses a recursive pattern.

  // the recursive function call is separated from main logic as it could be the case that one of the calls results in Infinity, which means no solution could be found and -1 needs to be returned as final answer.
  function coinChange(coins, amount) {
            const answer = _minChange(coins, amount);
            return answer === Infinity ? -1 : answer;
         }
        // Recursive call with memoization
         const _minChange = (coins, amount, memo = {}) => {
             // two base cases, either coin could not be used, more than amount
             if (amount < 0) return Infinity; 
             // or it is exact amount, so return from recursive call. Outside recursive call 1 is added to account for the edge in grpah.
             if (amount === 0) return 0;
 
             if (amount in memo) return memo[amount];

             let minChange = Infinity;
             // iterate over all coins and recursively call function to get either base case.
             for (let coin of coins) {
               const numCoins = 1 + _minChange(coins, amount - coin, memo)
               // Min value logic to ensure on ly the minimum branch (edges) counted gets returned from the recursive calls.
               minChange = Math.min(numCoins, minChange); 
             }
             // clever javascript trick, not intuitive but does assignment and return in on line.
             return memo[amount] = minChange;
         }

<p style="color:lightgreen">Exhaustive recursion</p>

This problem requires one to think about applying a decision tree to the inputs. Follow the steps for normal recursion where you identify the return value from the recursive call as well as the state you will recursively pass into the function, note that this state must get smaller and eventually result in a base case which allows you to return from the recursion.

```javascript example

const subsets = (elements) => { // base case is when no elemtns exist return empty subset if (!elements.length) return [[]]

// either take the first letter, or don’t take the first letter const first = elements[0]; const rest = subsets(elements.slice(1)) const restWithFirst = rest.map(a => [first, …a])

return […restWithFirst, …rest]

};

subsets([‘a’, ‘b’]);



#### [Generate parenthesis](https://leetcode.com/problems/generate-parentheses/)

This is a classic combinatorial problem which requires searching all combinations and backtracking using dfs.
- Think about your base case to populate one valid path. This is where drawing the state-space tree will help. 
- In this case it is when the accumulated path is equal to the 2 braces (2) * n;
- Update result, and return
- then the two recursive cases are either validly inserting a open brace or inserting a valid close brace.
- Then recursively call function, updating state, which is count of open or closed brace
- and backtrack, after recursive call, so pop()

__Javascript solution__ 

```javascript
    var generateParenthesis = function(n) {
        
        let result = [];
        const gen = (braces = [], open = 0, closed = 0) => {
            
        if (braces.length === 2 * n) {
            result.push(braces.join(""));
            return;
        } 
            
        if (open < n && open >= closed) {
            braces.push("(");
            gen(braces, open + 1, closed);
            braces.pop();
        }
            
        if (closed < n & open >= closed) {
            braces.push(")");
            gen(braces, open, closed + 1);
            braces.pop();
        } 
        }
        gen();
        return result;
    };

Word Break (Combinatorial problem using memoization)

        function wordBreak(s, words) {
            // used to store the previous solutions found in teh decision state-space-tree
            const memo = {};
            // kick off the function call, returning the result wither true or false, pass in previous args, as well as 0, to track the recursive end condition
            return dfs(s, words, 0, memo)
            
        }

        const dfs = (s, words, i, memo) => {
        // base case is if the length of the string is equal to the index i, then all options can fit in the original string
        if (i === s.length) return true;
        // short-circuit call if already seen this solution in the state-space-tree
        if (i in memo) return memo[i];  
            
        // track the found state
        let found = false;
        // classic dfs search algorithm, for...of with recursive call based on condition
        for (let word of words) {
            // start at the ith index and slice until the end of string, i.e whatever still needs to be checked
            // check if the string starts with the word, each word in list will be checked
            // if it does then recursively call the dfs function to check the rest of the string, and increase i to just after the previously found word in string
            if (s.slice(i).startsWith(word)) {
            if (dfs(s, words, i + word.length, memo)) {
                found = true;
                break;  
            };
            }
        }  
        memo[i] = found;
        return found;  
        }

Bottom up (tabulation)

Pattern of recurrence

This is used for bottom up approach to solving dp problems. The recurrence relation can be formulated as such:

      dp[i] = dp[i - 1] + dp[i - 2];

House Robber

This is a sequence type dp problem that can be solved with the pattern of recurrence. The keywords max, and array indicate solved using dp. The below uses a bottom up (tabulation) approach to get the answer

Pseudocode

        function rob(nums) {
            
            // edge case if no items
            if (nums.length === 0) return 0;
            // base case if only 1 or two items, can only select the max from both
            if (nums.length < 2) {
            return Math.max(nums)
            }
            const n = nums.length
            // start with 0s at each house
            const dp = Array(n).fill(0);
            // populate first house, and second house is max of either itself or previous house. Adjacent house cannot be counted together
            dp[0] = nums[0];
            dp[1] = Math.max(nums[0], nums[1]);
            // iterate and apply pattern of recurrence
            for (let i = 2; i < n; i++) {
            // make sure you are taking previous values from dp list not from nums array. as the dp array values are ones being changed.
            dp[i] = Math.max(dp[i - 1], (nums[i] + dp[i - 2]));
            }
            return dp[dp.length - 1];
        }

Largest divisible subset

Things to take away

//SOLUTION USES BOTTOM UP DP APPROACH
function findLargestSubset(nums) {
  
  // the problem requires a sorted set of distinct numbers for the DP algorithm 
  nums.sort((a,b) => a - b);
  // often in DP bottom up will require some state, usually an array to keep answers
  const maxSubsets = [];
  for (let i = 0; i < nums.length; i++) {
    // restart the max subset count each time the largst next value in nums is assessed
    let maxSubset = 0;
    // assess each value (that is smaller due to sorting) from largest next value by dividing it
    for(let j = 0; j < i; j++) {
      // this console log shows how answer is built up  
      console.log(`${nums[i]} divided by ${nums[j]} = ${nums[i] % nums[j]}, i:${i}, j:${j}, maxSubsets is ${maxSubsets}`);     
      // check last largest value, against all previous (smaller) values if they divide with no remainder  
      if (nums[i] % nums[j] === 0) {
          maxSubset = Math.max(maxSubset, maxSubsets[j])
      }
    }
    // the plus one is important
    maxSubsets.push(maxSubset + 1)
  }
  return Math.max(...maxSubsets)

}

console.log(findLargestSubset([1,2,4,8]))

## Dynamic programming - grid format problems

### Number of paths #### approach

  1. think about r and c being passed in every recursive call, default r = 0, c = 0, think about return type
  2. Test for out of bounds to the right and down, r === graph.length, c === graph[0].length, return 0, ensure you cano only index into grid if in bounds
  3. base case is if r === grid.length - 1, and c === grid[0].length - 1 , return 1, one way to traverse
  4. recursively call function, with r + 1, then another call with c + 1
  5. make sure you add them together, to sum number of ways.
  6. memoize function recording r and c as string in memo
      // recursive solution top-down with memoization
      function uniquePaths(m, n) {

        const traverse = (r,c, memo = {}) => {
            const pos = `${r},${c}`
            if (pos in memo) return memo[pos]
            if (r > m || c > n) return 0;
            if (r ===m && c === n)  return 1;
            return memo[pos] = traverse(r + 1, c) + traverse(r, c + 1);  
          }

          return traverse(1,1)
      }

The grid type dp probem can also be solved with bootom up approach using tabulation. NOTE using new Array(SIZE_ROW_OR_COL).fill(1) syntax

      function uniquePaths(m, n) {

        const dp = [];
        for (let i = 0; i < m; i++) {
          dp.push([...new Array(n).fill(1)])
        }

        for (let i = 1; i < m; i++) {
          for (let j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

          }
        }

        return dp[m - 1][n - 1]
      }

Maximal Square Key [dp, grid]

      function maximalSquare(matrix: string[][]): number {
          // first get the length of the rows
          const m = matrix.length;
          // and the length of the cols
          const n = matrix[0].length;

          // build the auxilliary array, watch out for out of bounds of by one error
          // note we add 1 to the rows and cols when building the dp[][] array
          const dp = Array(m + 1).fill(0).map(() => Array(n + 1).fill(0));
          // start with assuming zero and build up
          let max = 0;
          // iterate through the rows
          for (let i = 1; i <= m; i++) {
              // and cols
              for(let j = 1; j <= n; j++) {
                  // check the original matrix, only consider valid entries where the top-left block has a one
                  if (matrix[i - 1][j - 1] === "1") {
                      // this is the key line, it is the pattern of reccurence
                      // complete the dp table with the minimum of the previous assessed entries.
                      // catch here is to assess the actual dp table NOT the original matrix. Here you are building up numbers
                      // return the minimum of the top-left, top and left entries, then add 1
                      // another CATCH, do not forget to add 1, to indicate you found another square
                      dp[i][j] = Math.min(Number(dp[i - 1][j]), Number(dp[i][j - 1]), Number(dp[i - 1][j - 1])) + 1;
                      // update the max size square length, classic max sum logic here
                      max = Math.max(max, dp[i][j])

                  } 
              }
          }
          // finally return the square length as a square, so the max value squared.
          return max ** 2;

      };

      maximalSquare(
      [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]])

Interval type problems

Merge intervals

#### [Pattern to merge lsit of lists with intervals](https://algo.monster/problems/merge_intervals)

- Start with first sorting the lists, usually the start time should be sorted. This can be done trivially using the sort function in Python.
- Write a helper function that takes two lists and returns True or False if there is an overlap.
- Iterate over the list of lists, and either append a new interval if the result list is empty (i.e. needs a first interval to start) or there is no overlap.
- If there is a overlap, replace the result ending interval with the max of wither the current interval end, or the new interval being iterated over, its end time.

see Algo monster for a solution.

Systems design type problems

Rectangular Love

The below problems still need to be placed in the correct spots above

Reverse words in a string

Longest Palindromic substring

  1. This problem can be solved using dynamic programming
  2. In an interview setting the easier option is to use the expand from middle technique and loop over the string (0(n^2) is best case
  3. The brute force solution is easiest to solve it but very poor performance n^3
  4. Be careful of the classic index +1 problem

Roman to Integer challenge ✔️

isPalindrome ✔️

Matching Parens

Coin Change

### Remove duplicates from Sorted Array 🚩 ✔️

Median of two sorted arrays 🚴‍♂️

Reverse Integer

Container with most water 🚩

Zigzag Conversion

Regular Expression Matching